The Number of Realizations of a Laman Graph
Jose Capco,
Matteo Gallet,
Georg Grasegger,
Christoph Koutschan,
Niels Lubbes,
Josef Schicho
Johann Radon Institute for Computational and Applied Mathematics (RICAM)
Austrian Academy of Sciences (ÖAW)
Research Institute for Symbolic Computation (RISC)
Johannes Kepler University Linz (JKU)
Abstract
Laman graphs model planar frameworks that are rigid for a general choice of distances between the vertices. There are finitely many ways, up to isometries, to realize a Laman graph in the plane. Such realizations can be seen as solutions of systems of quadratic equations prescribing the distances between pairs of points. Using ideas from algebraic and tropical geometry, we provide a recursive formula for the number of complex solutions of such systems.Material
- The Paper appeared in the SIAM Journal on Applied Algebra and Geometry. Here is a Preprint that is also available as arXiv:1701.05500
- Slides of a talk given by C. Koutschan at the SFB F50 meeting in Vienna (extended version of the slides presented at MICA 2016).
- Slides of a talk given by J. Schicho at the workshop Unusual Configuration Spaces
- We have also presented our work at the Banff workshop Computational Algebra and Geometric Modeling.
Algorithm
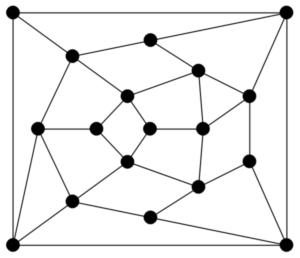
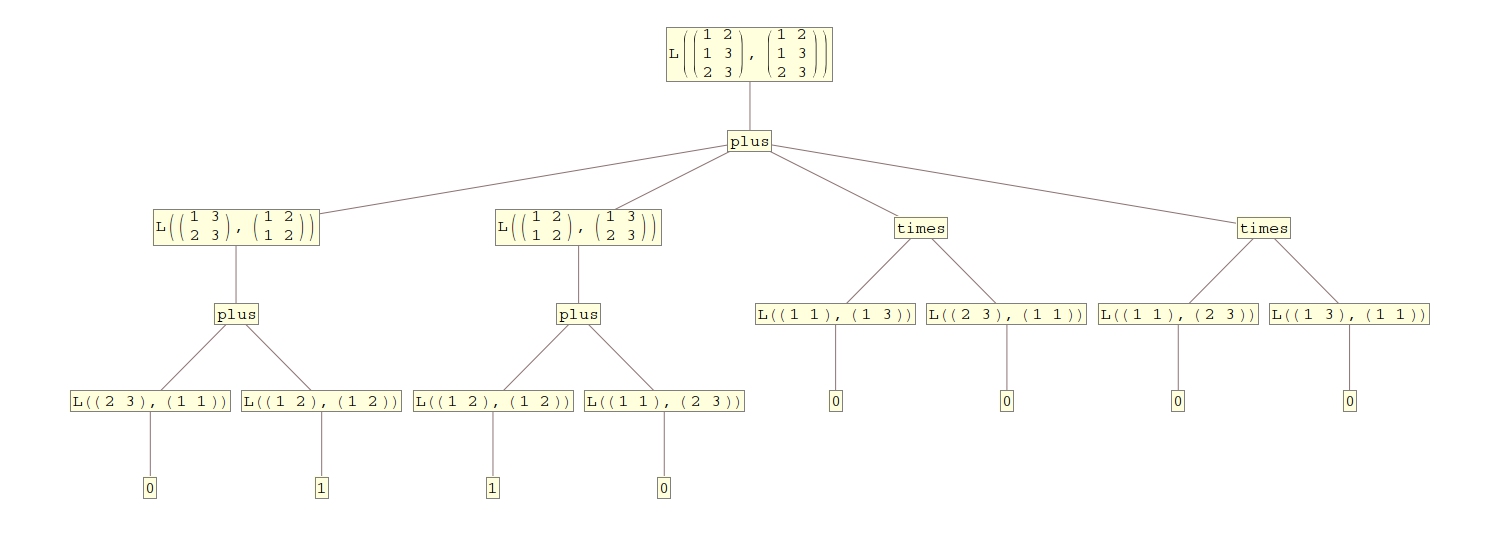
The algorithm is sketched in our working notes. Here we show an example of a computation tree; due to the complexity of the algorithm, we use a very simple example, namely the bigraph consisting of two triangles. The result is 2, which is indeed the Laman number of the triangle. By L(G,H) we denote the Laman number of the bigraph (G,H), and a graph here is given by its edges: each row of the n×2 matrix contains two vertices that are connected by an edge.Real Embeddings of the Three-Prism Graph
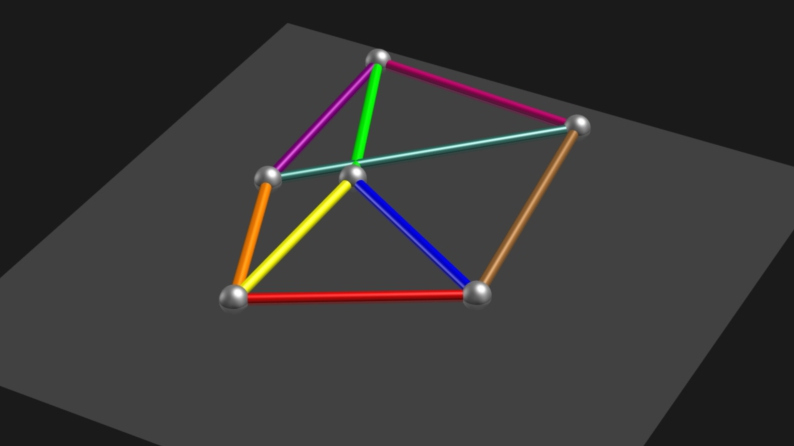
An interesting question is whether one can find as many real embeddings of a Laman graph as is given by its Laman number; the latter counts the number of its complex embeddings. For the three-prism graph we found an assignment of the edge lengths $$z_{1,2}=2,z_{1,3}=2,z_{2,3}=2,z_{1,4}=\tfrac{7}{4},z_{3,6}=\tfrac{27}{10},$$ $$z_{2,5}=\tfrac{197}{100},z_{4,5}=\tfrac{11}{5},z_{4,6}=\tfrac{29}{10},z_{5,6}=\tfrac{43}{20}$$ such that all its 24 embeddings are real. Below we show 12 of them, the remaining 12 ones are obtained by reflection across the vertical axis. Remarkably enough, when building a mechanical device with the above lengths (see the figure below), all 12 configurations can be reached without disassembling the linkage. This is shown in the animation.Software
The algorithms described in our paper have been implemented in the computer algebra system Mathematica and in C++.-
LamanGraphs.m (Mathematica source code;
Copyright © 2016 Christoph Koutschan)
- LamanGraphs.nb (Mathematica notebook)
- LamanGraphs.pdf (pdf screenshot of the notebook)
- laman.zip (C++ implementation for enumerating Laman graphs; Copyright © 2016 Jose Capco)
- laman.cpp (C++ implementation for computing Laman numbers; Copyright © 2017 Christoph Koutschan)
- lnumber.tar.gz (Most recent version of Capco+Koutschan's C++ implementation from the svn repository)
- Implementation of the algorithm (under the DOI 10.5281/zenodo.1245506).
- Data set containing all Laman graphs up to 12 vertices and their Laman numbers (under the DOI 10.5281/zenodo.1245517).
| Contact: | Visitors: |

 (
(