Exact lower bounds for monochromatic Schur triples and generalizations
Christoph Koutschan and Elaine Wong
Abstract
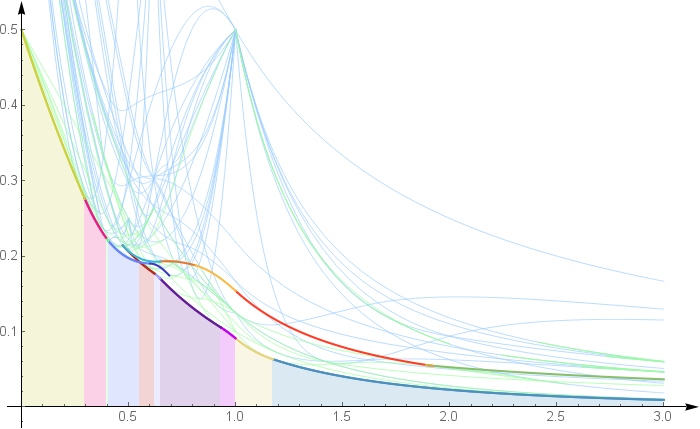
We derive exact and sharp lower bounds for the number of monochromatic generalized Schur triples $(x,y,x+ay)$ whose entries are from the set $\{1,\dots,n\}$, subject to a coloring with two different colors. Previously, only asymptotic formulas for such bounds were known, and only for $a\in\mathbb{N}$. Using symbolic computation techniques, these results are extended here to arbitrary $a\in\mathbb{R}$. Furthermore, we give exact formulas for the minimum number of monochromatic Schur triples for $a=1,2,3,4$, and briefly discuss the case $0< a< 1$.Paper
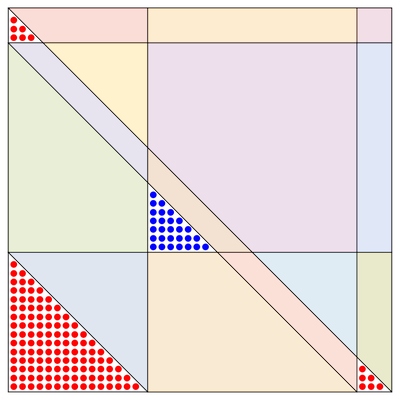
The material on this webpage accompanies the article Exact lower bounds for monochromatic Schur triples and generalizations by Christoph Koutschan and Elaine Wong.A triple $(x,y,z)\in\mathbb{N}^3$ is called a Schur triple if its entries satisfy the equation $x+y=z$. A coloring of the set $\{1,\dots,n\}$ is a map that assigns to each element a color (red or blue). We say that a Schur triple is monochromatic (with respect to a given coloring) if all of its entries have the same color. We are interested in the coloring that produces the least number of monochromatic Schur triples. For this purpose, we study colorings of the form $R^sB^{t-s}R^{n-t}$, i.e., the first $s$ numbers are red, the numbers $\{s+1,\dots,t\}$ are blue, and the remaining numbers are again red. Below the situation is depicted for $n=44$, and for the optimal choice $s=16$ and $t=40$. Each monochromatic triple $(x,y,x+y)$ is represented by a dot at position $(x,y)$. The shaded regions indicate the location of non-monochromatic triples.

Supplementary electronic material
We provide a Mathematica notebook- SchurTriples.nb (Mathematica notebook, last update 02.04.2019)
- SchurTriples.cdf (Mathematica computable document)
- SchurTriples.pdf (pdf printout of the notebook)
Contact: