Planar Linkages Following a Prescribed Motion
Matteo Gallet,
Christoph Koutschan,
Zijia Li,
Georg Regensburger,
Josef Schicho,
Nelly Villamizar
Johann Radon Institute for Computational and Applied Mathematics (RICAM)
Austrian Academy of Sciences (ÖAW)
Research Institute for Symbolic Computation (RISC)
Johannes Kepler University Linz (JKU)
Abstract
Designing mechanical devices, called linkages, that draw a given plane curve has been a topic that interested engineers and mathematicians for hundreds of years, and recently also computer scientists. Already in 1876, Kempe proposed a procedure for solving the problem in full generality, but his constructions tend to be extremely complicated. We provide a novel algorithm that produces much simpler linkages, but works only for parametric curves. Our approach is to transform the problem into a factorization task over some noncommutative algebra. We show how to compute such a factorization, and how to use it to construct a linkage tracing a given curve.The paper is published in Mathematics of Computation (DOI: 10.1090/mcom/3120). Here is the preprint version.
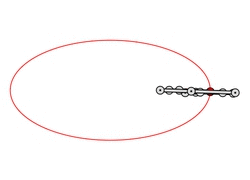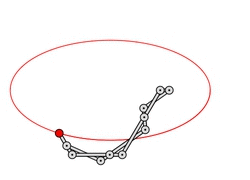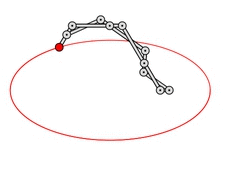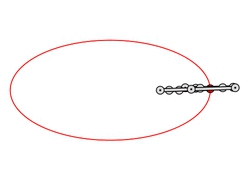
Example 1: Ellipse
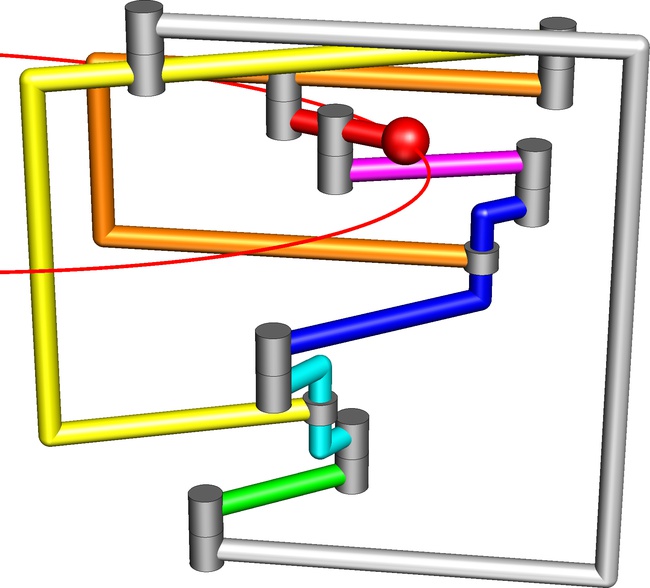
We first consider the ellipse defined by the equation (x + 1)2 + 4y2 = 1, i.e., its center is (-1, 0) and its radii are 1 and 1/2. Our algorithm ConstructStrongLinkage applied to the parametrization (-2, t) / (t2 + 1), yields a linkage with 10 links and 13 joints, which realizes a translational motion along the ellipse. If we skip the requirement that the motion is a translational one, i.e., if we just want to draw the ellipse, we can obtain an even simpler linkage, namely one with only 8 links and 10 joints (see the animation):
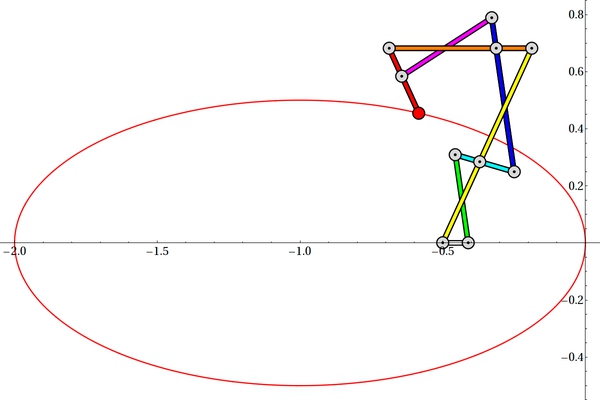
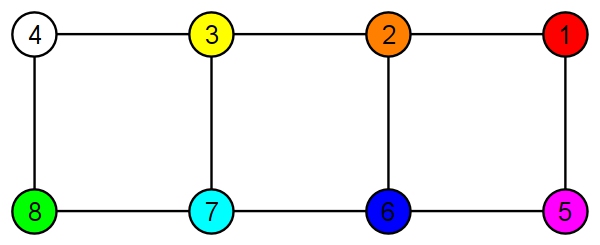
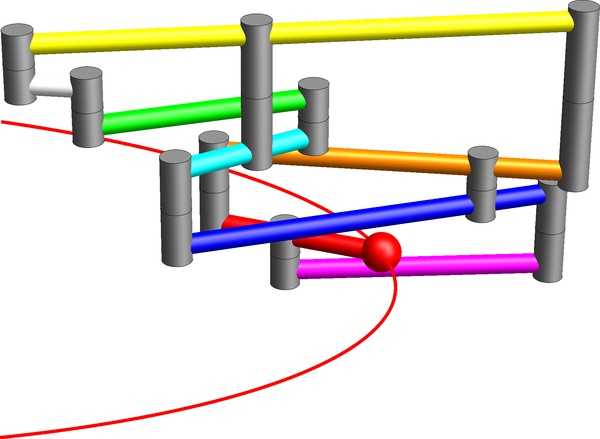
F-links) which are just straight rods located in a single layer. The linkage shown here has three F-links (green, red, magenta), three U-links (white, yellow, orange), and two Z-links (cyan, blue). See also the animation.
Example 2: John Hancock's J
Next we present an example in connection with a popular formulation of
Kempe's Theorem, stating that There is a linkage that signs your name. Henry King attributes this formulation to William Thurston. On the other hand, as remarked by Joseph O'Rourke, it is very implausible that a concrete
signing linkagehas ever been constructed due to the complexity, in terms of links and joints, of the linkages produced by Kempe's procedure. As an example to support his claim, O'Rourke points out that already constructing a linkage drawing the
Jof John Hancock's famous signature would be very difficult. We approximate this letter by a rational curve that is given by a parametrization of the form (f/h, g/h) where f,g,h are polynomials of degree 5,5,6, respectively. Our implementation of the algorithm ConstructStrongLinkage, which we develop in the paper, produces a linkage with 26 links and 37 joints drawing this curve. The motion it realizes is a translation, which we visualize by using a quill pen whose shape is a line segment in direction (5,6). The spatial arrangement of the links is indicated by hue: darker links lie below brighter ones (see the animation).
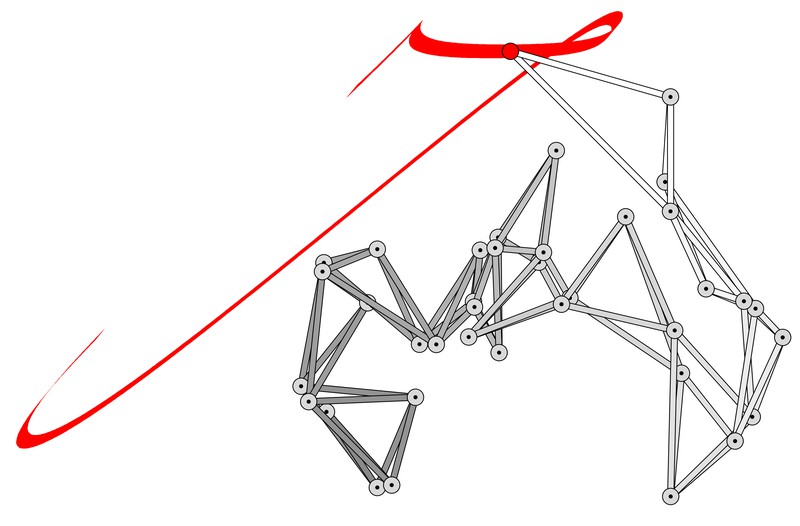
J, seven self-collisions occur. However, they are hardly visible, even in a 3D animation. The picture below shows the linkage at position t = –0.319038; we observe three collisions, namely the yellow link collides with the joint connecting blue and red, the red link collides with the joint connecting yellow and green, and the orange link with the joint connecting the two cyan links.
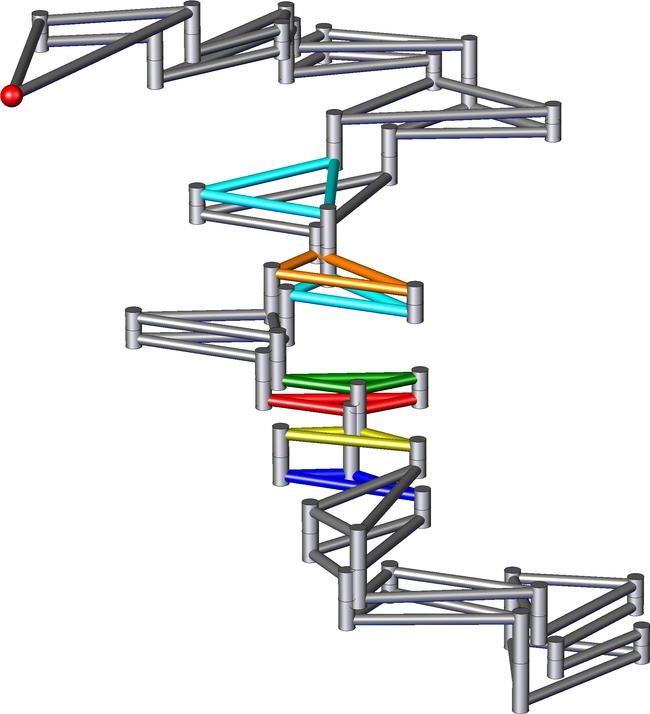
Example 3: Astroid
The astroid is a star-like curve with four cusps that is obtained by rolling a circle of radius 1 inside a circle of radius 4. After the small circle is back to its original position (after travelling clockwise, say), it has performed three counter-clockwise revolutions. Hence we can obtain its motion by composing a clockwise revolution around the origin with four counter-clockwise revolutions (one to compensate the clockwise rotation!) around the point (3,0). This yields a motion polynomial of degree 5. In the animation, this decomposition of the motion can be we well observed: the black link is fix, i.e., it moves according to the identity (corresponding to zero linear factors). The brown link performs the clockwise revolution. The red link performs a circular translation, corresponding to the composition of one clockwise and one counter-clockwise revolution. The orange, yellow, and white link make one, two, resp. three counter-clockwise revolutions at the same time, corresponding to the product of three, four, resp. five linear factors.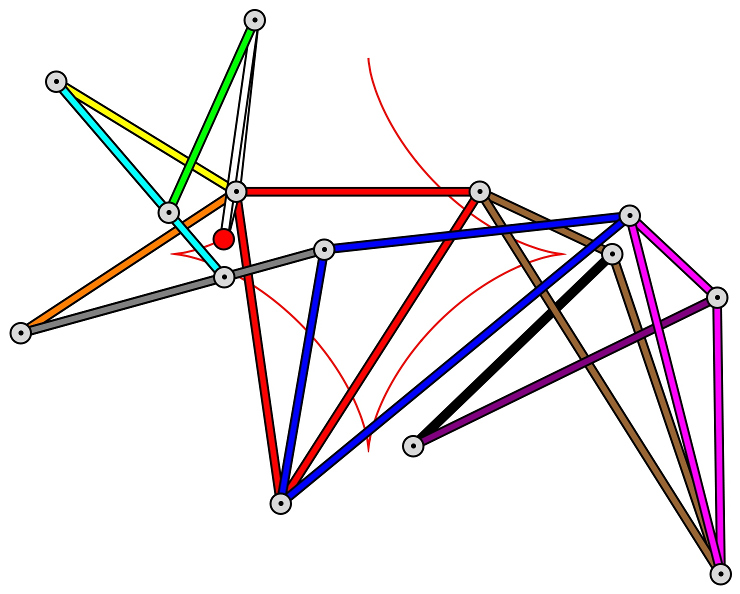
Animations
Here we list again all videos that were mentioned above, showing the linkage drawing an ellipse and the linkage signing aJ.
- Ellipse.mp4 (426 KB)
- Ellipse3D.mp4 (491 KB)
- EllipseCF3D.mp4 (802 KB)
- HancockJ.mp4 (827 KB)
- HancockJ3D.mp4 (2.6 MB)
- Astroid.mp4 (1.3 MB)
- fig8b_3d.mp4 (248 KB)
Software
All algorithms described in our paper have been implemented in the computer algebra system Mathematica, e.g., the factorization algorithm for motion polynomials and the construction of linkages with mobility one. In the notebook below we have collected a few instructive examples and the commands that produce some of the above pictures and animations. At ISSAC 2016, our software was awarded with the Distinguished Software Demonstration Award.-
PlanarLinkages.m (Mathematica source code;
Copyright © 2015 Christoph Koutschan)
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
- PlanarLinkages.nb (Mathematica demo notebook)
- PlanarLinkages.pdf (pdf screenshot of the notebook)
- PlanarLinkages.pdf (short article describing the package)
| Contact: | Visitors: |