Fundamental Laser Modes in Paraxial Optics: From Computer Algebra and Simulations to Experimental Observation
Christoph Koutschan, Erwin Suazo, Sergei K. Suslov
Abstract
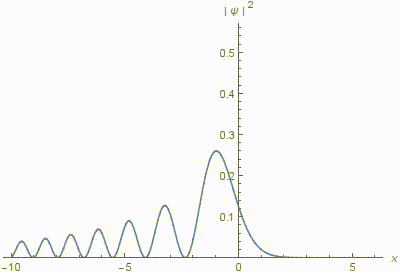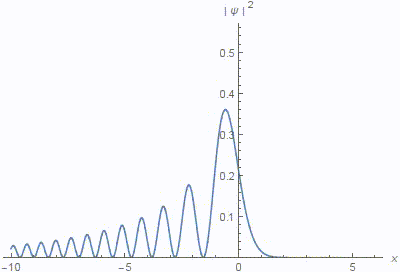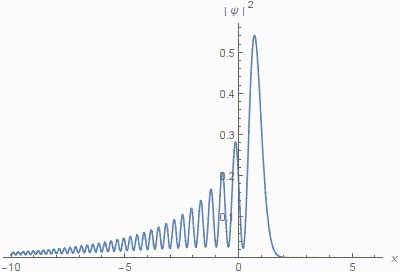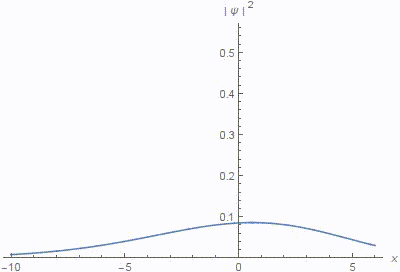
We study multi-parameter solutions of the inhomogeneous paraxial wave equation in a linear and quadratic approximation which include oscillating laser beams in a parabolic waveguide, spiral light beams, and other important families of propagation-invariant laser modes in weakly varying media. A "smart" lens design and a similar effect of superfocusing of particle beams in a thin monocrystal film are also discussed. In the supplementary electronic material, we provide a computer-algebra verification of the results presented here, and of some related mathematical tools that were stated without proofs in the literature. We also demonstrate how computer algebra can be used to derive some of the presented formulas automatically, which is highly desirable as the corresponding hand calculations are very tedious. In numerical simulations, some of the new solutions reveal quite exotic properties which deserve further investigation including an experimental observation.Paper
Read the full paper here.Supplementary electronic material
- MultiParameterModes.nb (Mathematica notebook)
- MultiParameterModes.pdf (pdf screenshot of the notebook)
Contact: